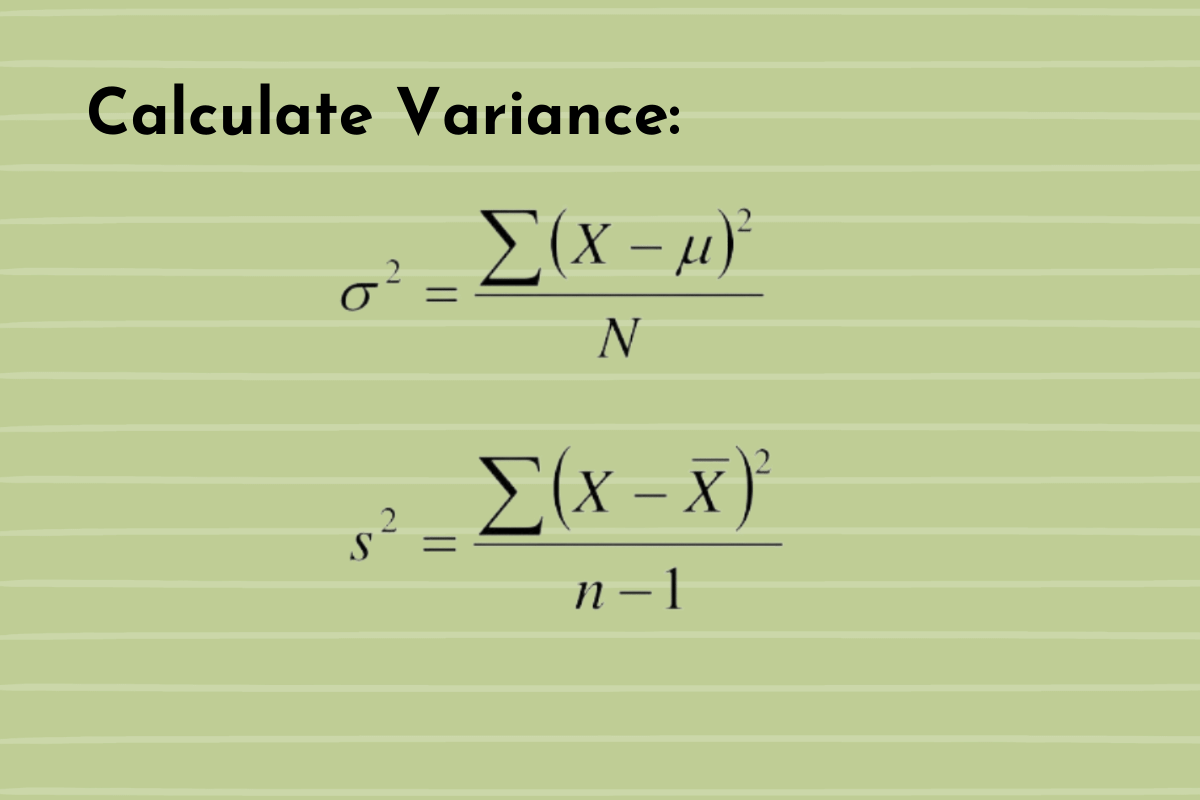Have you ever looked at a group of numbers and wondered how much they really differ from one another? You know, like if you're checking out how many steps people in your neighborhood walk each day, or perhaps the range of scores on a recent test. It's not just about the average, is that right? We often want to get a sense of how spread out those individual figures are from that average point. This idea of spread, or how much things tend to vary, is actually quite important in many everyday situations, even if we don't always think of it that way.
Getting a good grasp on how numbers are scattered can tell us a whole lot more than just knowing the middle value. For instance, if two groups have the same average, but one group's numbers are all very close together while the other's are wildly different, that's a pretty big distinction, isn't it? Knowing this difference helps us make better sense of information, whether it's about predicting outcomes or simply understanding a collection of facts. This is where a particular statistical idea, known as variance, truly helps us out.
Variance gives us a numerical way to describe that spread, offering a clearer picture of how much individual pieces of data tend to move away from the central point. And how do we figure this out? Well, there's a specific calculation for it, often called the variance formula. It’s a tool that helps us put a number on how much things jump around, providing a single figure that tells us a lot about the consistency, or lack thereof, within a group of observations.
- Karen Mean Girls
- Fondos De Pantalla Aesthetic
- Hillsong Worship What A Beautiful Name
- Watch 365 Days
- Rita Ora
Table of Contents
- What is the Variance Formula and Why Does it Matter?
- How does the variance formula show spread?
- Different Flavors of the Variance Formula- Population Versus Sample
- Unpacking the population variance formula
- Getting to know the sample variance formula
- How Do We Calculate the Variance Formula?
- The variance formula for ungrouped data
- Can a variance formula calculator help?
- What Else Connects to the Variance Formula?
What is the Variance Formula and Why Does it Matter?
When we talk about a set of numbers, we usually want to know more than just the average. We also want to know how much those numbers stretch out from that average. Variance is a way to measure this stretch. It's a single number that tells us how much individual items in a collection of data tend to stray from the typical value. This measurement is actually pretty useful because it helps us see if our numbers are all squished together or if they are spread out quite a bit. For instance, if you're looking at the heights of people in a room, you might find that most are close to the average, or you might find a mix of very short and very tall individuals, you know? Variance helps put a number on that observation.
The basic idea behind variance is to figure out how far each individual data point sits from the average value of the whole group. Then, we square those distances. Why square them? Well, if we just added up the distances, some would be positive and some negative, and they might cancel each other out, giving us a misleading zero. Squaring makes all the distances positive, so they add up properly to show the total spread. After squaring, we take an average of these squared distances. This final average is what we call variance. It gives us a sense of the typical squared distance from the average, which, in some respects, is a pretty good indicator of how much things differ.
How does the variance formula show spread?
Think of it this way: if your variance number is small, it means that most of your data points are quite close to the average. They don't stray too far. This suggests a group of numbers that are pretty consistent with each other. On the other hand, if you get a large variance number, it tells you that your data points are scattered widely across the board. Some are much higher than the average, and some are much lower. This indicates a lot of variety or difference within your group. So, a bigger variance means more spread, and a smaller variance means less spread, you see. This simple idea helps us compare different groups or understand the consistency of a single group.
Different Flavors of the Variance Formula- Population Versus Sample
When we talk about variance, there are actually two slightly different ways we might calculate it, depending on what kind of data we have. We might be looking at an entire collection of things, which we call a population. Or, we might only have a smaller piece of that collection, a subset, which we call a sample. The way we figure out the variance formula changes just a little bit between these two situations. It's a subtle but important distinction that helps us get the most accurate picture from our numbers.
Unpacking the population variance formula
If you have every single piece of data you could possibly have for a group – say, the heights of every single person in a city – then you're working with a population. For this, the variance formula is quite direct. You take each individual height, subtract the average height of everyone in the city, and then square that result. You do this for every single person. After that, you add up all those squared differences. Finally, you divide that sum by the total number of people in your population. This gives you the population variance. A common way to describe this is "the mean of squares minus the square of means," which is a specific mathematical way to get to the same result for a whole population, you know.
This population calculation assumes you have full knowledge. Sometimes, you might not know the exact values of every single item in your group, but you might know the average value. Even in those cases, the idea of how far things are from that known average still applies to figuring out the spread. For example, if you have two distinct groups, let's call them group M and group N, you might find that group M has a certain amount of spread, let's say a variance of $\sigma_m^2$, while group N has its own spread, perhaps $\sigma^2_n$. These figures help us compare how consistent each group is on its own.
Getting to know the sample variance formula
Now, what if you don't have all the data? What if you just have a small group of people from that city, like a sample, and you want to use their heights to guess the variance of the whole city? This is where the sample variance formula comes in. It's very similar to the population one, but with a tiny adjustment. You still take each height in your sample, subtract the average height of your sample, and square the result. You still add all those squared differences together. But here’s the difference: instead of dividing by the total number of people in your sample, you divide by one less than that number. This small change, dividing by (n-1) instead of n, helps to give you a better, less biased guess about the true variance of the larger population from which your sample came. It’s a way to make your sample variance a little more accurate as a stand-in for the whole group, you see.
There seems to be, in some respects, a general agreement on this approach for sample variance because it tends to give us a more reliable estimate. When we talk about how good our estimates are, sometimes we look at something called Mean Squared Error, or MSE. Interestingly, MSE can be broken down into parts that include variance and something called bias. The way variance fits into this decomposition helps us understand the quality of our predictions or estimates. So, while it might seem like a small detail, the difference between population and sample variance is actually pretty important for getting accurate statistical pictures.
How Do We Calculate the Variance Formula?
Figuring out variance can seem a little complicated at first, but it’s actually a series of pretty straightforward steps. Whether you're doing it by hand or using a tool, the core idea stays the same. The goal is always to quantify how much your numbers are spread out from their average. Let's walk through the basic process, which, you know, is quite common for data that isn't already sorted into groups.
The variance formula for ungrouped data
For data that isn't already organized into categories or groups, the steps are quite clear. First, you need to find the average value of all your numbers. This average is your central point. Next, for each individual number in your set, you subtract that average. This tells you how far each number is from the middle. Some of these results will be positive, and some will be negative. After that, you take each of those differences and square it. This step is really important because it makes all the numbers positive and gives more weight to numbers that are further away from the average. Numbers that are really far out will have a much bigger squared difference, which means they'll have a bigger impact on the overall variance, you see.
Once you have all these squared differences, your next step is to add them all up. You get a total sum of all those squared distances. Finally, to get the actual variance, you take that total sum and divide it by the number of data points you have (or by one less than the number of data points if you're working with a sample, as we discussed). This division gives you the average of the squared differences, which is our variance. It’s a pretty systematic process that helps us get a solid numerical description of how spread out our data truly is.
Can a variance formula calculator help?
Absolutely! While it's good to understand the steps for calculating variance by hand, doing it for a large set of numbers can be quite a bit of work. This is where tools like a variance calculator come in handy. These calculators pretty much automate the whole process for you. You just enter your set of numbers, and the calculator does all the subtractions, squaring, summing, and dividing for you. Many of these tools don't just give you the variance; they also often provide the standard deviation (which is just the square root of the variance), the sample size, the mean, and even the sum of squares, you know.
Using a calculator for the variance formula can save a lot of time and help prevent small calculation mistakes. It's especially useful when you're dealing with many data points or when you need to quickly check the spread of different datasets. Some calculators even show you the step-by-step work they perform, which can be a great way to learn or double-check your own understanding of the process. So, while knowing the manual steps is important, there's no reason not to use technology to make things easier, is that right?
What Else Connects to the Variance Formula?
The variance formula isn't just a standalone calculation; it's connected to many other ideas in the world of numbers and statistics. For instance, one of its closest relatives is the standard deviation. The standard deviation is simply the square root of the variance. While variance gives us a squared measure of spread, standard deviation brings that measure back to the original units of our data, making it often easier to interpret. So, if your data is in meters, your variance would be in "square meters," but your standard deviation would be back in "meters," which is pretty helpful for understanding real-world distances.
Variance also plays a role in more complex statistical models. For example, when we try to predict something using a linear model, the variance of our predictions helps us figure out how much we can trust those predictions. It's a way to put boundaries around our guesses, giving us a sense of how much our actual results might differ from what we expect. This helps us understand the uncertainty in our models. There's also the idea of how variance is used in different types of distributions, like the Beta distribution, where knowing the average and the variance can help describe the shape of how numbers are spread out between zero and one.
Sometimes, there can be a bit of confusion around weighted variance, especially when different parts of your data might have different levels of importance. But generally, there's a pretty clear understanding of how to approach these situations, which helps make sure our calculations are fair. In essence, the variance formula provides a numerical way to tell how much individual items in a group tend to spread out from their average value. A smaller variance means the data points are very close to the average, showing consistency. A larger variance means the data points are scattered widely, showing a lot of variety. It’s a fundamental tool for making sense of how numbers behave.